Chaotic Invariants of Lagrangian Particle Trajectories for Anomaly Detection in Crowded Scenes

Related Publication: Shandong Wu, Brian Moore, and Mubarak Shah, Chaotic Invariants of Lagrangian Particle Trajectories for Anomaly Detection in Crowded Scenes, IEEE Conference on Computer Vision and Pattern Recognition 2010, San Francisco, CA.
　

Abstract

A novel method for crowd flow modeling and anomaly detection is proposed for both coherent and incoherent scenes. The novelty is revealed in three aspects. First, it is a unique utilization of particle trajectories for modeling crowded scenes, in which we propose new and efficient representative trajectories for modeling arbitrarily complicated crowd flows. Second, chaotic dynamics are introduced into the crowd context to characterize complicated crowd motions by regulating a set of chaotic invariant features, which are reliably computed and used for detecting anomalies. Third, a probabilistic framework for anomaly detection and localization is formulated.

The overall work-flow begins with particle advection based on optical flow. Then particle trajectories are clustered to obtain representative trajectories for a crowd flow. Next, the chaotic dynamics of all representative trajectories are extracted and quantified using chaotic invariants known as maximal Lyapunov exponent and correlation dimension. Probabilistic model is learned from these chaotic feature set, and finally, a maximum likelihood estimation criterion is adopted to identify a query video of a scene as normal or abnormal. Furthermore, an effective anomaly localization algorithm is designed to locate the position and size of an anomaly. Experiments are conducted on known crowd data set, and results show that our method achieves higher accuracy in anomaly detection and can effectively localize anomalies.

　
l

Significance of Crowd Scene Analysis

  • lManagement of large gatherings of people at events or in confined spaces

  • lAnomaly detection, localization, and alarm

  • llCrowd surveillance, public place monitoring, security control, etc.

Figure 1. Crowd scenarios with different levels of coherency.
　
l
Challenges

  • lVery high density of objects

  • Diverse level of coherency of motions

  • Traditional methods

  • Only suitable for sparse scenes

  • Suffer from the problems due to severe occlusions, small object sizes, similar appearance

The Idea

  • Lagrangian particle dynamics + chaotic invariants

Figure 2. Framework for anomaly detection and localization.

　

The Novelties

  • Unique utilization of clustering of particle trajectories for modeling crowded scenes

  • Chaotic dynamics are introduced into the crowd context

  • Being able to deal with both coherent and incoherent flows

　

Particle Advection

      

   

Figure 3. Particle trajectories overlayed on three crowd scenes. Top row shows zoom-in view of parts of each scene.

　

l

Cluster Particle Trajectories

  • Principle: A bunch of adjacent particle trajectories may belong to a single sub-object

  • Method: clustering

        Step 1: Remove relatively motionless particles and trajectories that carry minor information

        Step 2: Cluster by k-means according to position information

        Output: Representative trajectories

    　

    Figure 4. Trajectories after low variance particles are removed. Top row shows zoom-in view of parts of each scene.  

     

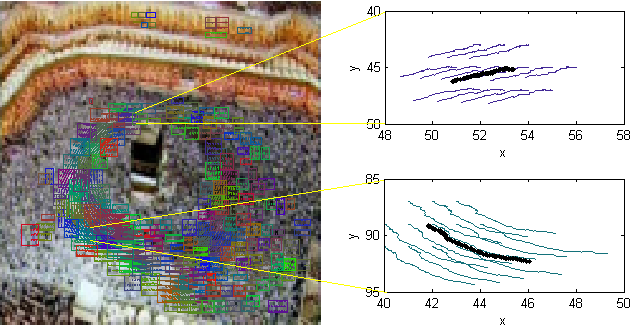
    Figure 5. Trajectories clustered according to position information, (left) and representative trajectories for two clusters (right).

      

    Figure 6. Representative trajectories for three scenes. Top row shows zoom-in view of parts of each scene.

l
Chaotic Invariants

  • Representation of scenes: Representative trajectories

  • To identify the scene¨s dynamics in terms of the dynamics of representative trajectories: lChaotic dynamics by measurable chaotic invariants

　
Feature Set

    F = { L, D, M }

  • L: Largest Lyapunov exponent
  • lD: Correlation dimension
  • lM: Mean of representative trajectories (Only necessary for position-caused anomalies)

        

    Figure. The algorithm for computing L and D.

     

Advantages of the Algorithm

  • lProven to be insensitive to the changes in time delay, embedding dimension, size of data set and to some extent noise
  • lEnsure L>0 for condition of chaotic analysis

Figure 7. Largest Lyapunov exponents for representative trajectories using our method (left) and the method of [7] (right).

　

　
l
Anomaly Detection
  • Definition of anomaly: Spatiotemporal change of scene/system dynamics (chaotic or/and positions)
      Global anomaly: entire change of dynamics
      Local anomaly: dynamics changes near particular spatial points
  • Approach: Probabilistic model
    　
Modeling Learning
  • lNormality model: Multi-variate GMM
  • Learning by: EM + IPRA algorithm 
  • Principle for judging a query as normal or abnormal: Probability of the query belonging to the normality model  + ML criterion

    　

Anomaly Localization

  • Localize the anomaly in terms of position & size.
  • Steps:
    • Calculate the likelihoods contributed by each representative trajectory
    • Localize those trajectories with low likelihoods
    • Cluster them according to position information
    • Filter out the clusters with fewer number of trajectories
    • The remaining clusters reveal the major abnormal regions
　
　
Experiment Results
  • Dataset

    Unusual crowd activity dataset from University of Minnesota

    Other coherent and incoherent crowd motions

    10-frames clips and interpolate to 500 points

    　

  • Three experiments
Global anomaly detection (Exp. 1)

Figure 8. Sample frames from three crowd scenes. The first two frames in each row show normal behavior, and the third frame shows abnormal escape panic

Figure 9. Representative trajectories for three clips in a sequence, the first one shows normal behavior and the last two are abnormal.

Figure 10. Marginal PDF of two chaotic features of x (left) and y (right) of learned 4-D mixture of Gaussian model.

Figure 11. Likelihood profile for testing clips and corresponding ground truth.

Figure 12. ROC curves for (a) our method, and (b) method of [9].

　

Due to change of chaotic dynamics (Exp. 2)

Figure 13. (a) Normal clapping behavior, and (b) introduction of abnormal dancing behavior.

Figure 14. For clip 30 correctly detected anomalies, red points below threshold correspond to abnormal representative trajectories, while blue points above threshold correspond to normal.

Figure 15. A frame from a clip with abnormal behavior, (a) representative trajectories, (b) candidates for local anomalies, (c) correct localization of anomalies.

　

Position-caused in consistent motions (Exp. 3)

Figure 16. Position-caused anomaly localization

　

Conclusions

  • lA novel combination of Lagrangian particle dynamics approach together with chaotic modeling.

  • Representative trajectory: serve as a compact, yet informative, modeling element in crowd flows.

  • A representative feature set to reliably capture the system dynamics.

  • An effective anomaly detection & localization algorithm.