Crowd Flow Segmentation

Crowd Flow Segmentation & Stability Analysis

Related Publication: Saad Ali and Mubarak Shah, A Lagrangian Particle Dynamics Approach for Crowd Flow Segmentation and Stability Analysis, IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), 2007.

Introduction
Algorithmic Steps
Downloads
Video Presentation
Related Links

Introduction

Video surveillance in public places is proliferating at an unprecedent rate, from closed-circuit security systems that can monitor individuals at airports, subways, concerts, sporting events etc., to network of cameras blanketing important locations within a city. Over the years, a number of intelligent surveillance systems have been developed for effective and efficient processing of the video footage generated by these surveillance cameras. However, despite the sophistication of these systems, they have not yet attained the desirable level of applicability and robustness required for the real-world settings and uncontrolled conditions. This is largely due to the algorithmic assumptions about the density of objects in a scene that are often violated in the real world environment. That is, the algorithms built into these systems assume that the observed scene will have a low density of objects. With video feeds from real-world settings like train stations, airports, city centers, malls, concerts, political rallies, sporting events, contain high to moderate density of crowds, simply being able to automatically and reliably detect, track and infer events remains a big hurdle for these surveillance systems.

To overcome this shortcoming, we have developed a framework that models the crowded scene at a global level and bypasses the low-level object localization and tracking altogether. This is achived by treating the crowded scene as a fluid flow where Lagrangian Particle Dynamics is employed to detect dominant crowd flow segments. The dynamical behavior of each flow segment is then modelled to infer any abnormal activity taking place within the crowd.

Algorithmic Steps

Given a video of a crowded scene, the first step is to compute the optical flow between consecutive frames. The optical flow fields are stacked up to generate a 3D volume. Next, a grid of Lagrangian particles is overlaid on the flow field volume, and advected using a numerical integration scheme. The evolution of particles through the flow is tracked using Flow Maps, which relate the initial position of the particles with their final position. The third steps computes gradients of the flow maps, and uses it to quantify the amount by which the neighboring particles have diverged by setting up a Cauchy-Green deformation tensor. The maximum eigenvalue of this tensor is used to construct the Finite Time Lyapunov Exponent (FTLE) field, which reveals Lagrangian Coherent Structures (LCS) present in the underlying flow. The LCS, which appeara as ridges in the FTLE field, divide the flow field into regions of qualitatively different dynamics and therefore can be used to locate the boundaries of the crowd flow segments. This is done by segmenting the FTLE field, which is a scalar field, in a normalized cuts framework. Finally, any change in the learned dynamics of the underlying flow is regarded as an instability, which is detected by signalling out new flow segments by establishing correspondence between flow segments over time. A brief description of each step along and associated results are provided in the following sections.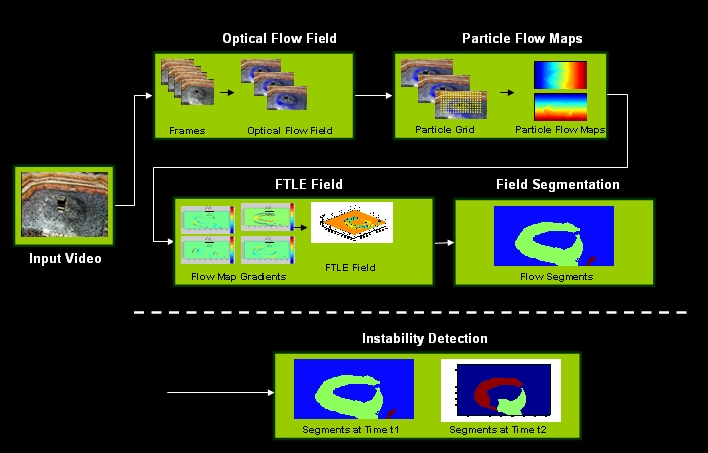

(a) The block diagram of the crowd flow segmentation and instability detection algorithm.

i) Optical Flow Computation

Given a video sequence containing crowds, the first task is to estimate the flow field. We employ a scheme consisting of block based correlation in fourier domain for this purpose. Here we show results of the optical flow computation on two sequences from our data set.

Video of the optical flow for the Mecca sequence.

Video of the optical flow for the Pilgrims sequence.

ii) Flow Map Computation

The next step is to carry out particle advection under the influence of the stacked up flow fields. To perform this step, a grid of particles is launched over the first the first flow field. The particles in the grid are advected usinga fourth order Runge-Kutta-Fehlberg algorithm. For the following sequences, we show two videos where first video depicts the evolution of the x-coordinate of the partciles, while the second video depicts the evolution of the y-coordinate of the particles.

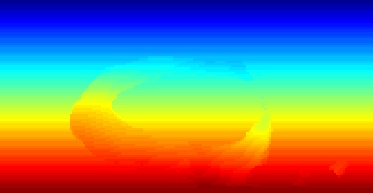X-Particle Flow Map Y-Particle Flow Map

iii) FTLE Field The FTLE field is computed from the flow maps computed in the last step. This is done by taking the spatial derivatives of the flow maps using a finite differencing approach. The amount by which the nearby particles have diverged from each other is quantified by setting up a Cauchy-Green deformation tensor. The maximum eigenvalue of the tensor is used to construct a Finite Time Lyapunov Exponent (FTLE) field, which reveals the Lagrangian Coherent Structures (LCS) present in the underlying flow field. The LCS appear as ridges in the FTLE, and divide the flow into regions of qualitatively different dynamics. The following figure shows a number of examples of LCS computed for different sequences from our data set.
Mecca Sequence FTLE Field	Victory Parade Sequence FTLE Field	Traffic Sequence FTLE Field	Pilgrims Sequence FTLE Field

iv) Segmentation The FTLE field is a scalar field that captures the underlying flow dynamics and geometry. For the segmentation of this scalar field, we employ the normalized cuts algorithm, first proposed by Shi et. al. Our segmentation procedure is composed of two main steps. The first step involves an over-segmentation of the given FTLE field. In the second step, we merge the segments whose boundary particles have similar behavior in Lyapunov sense. The final flow segmentations for a number of sequences are shown in the following figure. The different colors in the segmentation results represent different flow segments.
Mecca Sequence Crowd Flow Segments	Traffic Sequence Crowd Flow Segments	Victory Parade Sequence Crowd Flow Segments	Pilgrims Sequence Crowd Flow Segments

Mecca-2 Sequence Crowd Flow Segments	Traffic-2 Sequence Crowd Flow Segments	Pilgrims-2 Sequence Crowd Flow Segments	NYC Marathon Sequence Crowd Flow Segments

v) Flow Instability Detection Given flow segments, we define the problem of locating flow instability as detecting the change in the number of flow segments. Recall that in our flow segmentation framework, boundaries of the flow segments having different dynamics are reflected as LCS in the FTLE field. Due to this formulation any changes in the dynamic behavior of the flow will cause new LCS to appear in the FTLE field at exactly those locations where the change happens. These new LCS will eventually give rise to new flow segments which were not there before. By detecting these new flow segments, we will be in a position to identify the locations in the scene where the flow is changing its behavior. For detecting new flow segments, we establish correspondence between the flow segments which are generated from two consecutive blocks of the video. The correspondence is computed by modeling the shape of each segment and using a pixel based voting scheme. The testing is performed by introducing synthetic flow instabilities into the original video sequences.
Original Sequence Original Flow Segments	Sequence with synthetic instability New Flow Segments	Original Sequence Original Flow Segments	Sequence with synthetic instability New Flow Segments

Downloads

Dataset used in the CVPR 2007 paper. [22MB]
Slides of the Talk Given at CVPR 2007. [57MB]
Matlab Code including Examples [630MB] This Matlab code is an extended/modifed version of the code used in the CVPR paper. You can read about the extension in my thesis which is available at my homepage. The code is provided as is for research purposes only, with no warrantee. The code is self explanatory, and I have provided two data sets for users to have it up and running. The starting script is 'go_segmentation.m'. User can select one of the two videos by making selection at the top this script file. Please do not contact me for assistance with installing, understanding or running the code. However, if you find some bug, drop me an email.
Complete Dataset [128MB]. The data set contains videos of crowds and other high density moving objects. The videos are collected mainly from the BBC Motion Gallery and Getty Images website. The videos are shared only for the research purposes. Please consult the terms and condition of use of these videos from the respective websites. The keyframes of the videos in the data set are shown below. If you happen to use the data set, please refer the following paper:

Saad Ali and Mubarak Shah, A Lagrangian Particle Dynamics Approach for Crowd Flow Segmentation and Stability Analysis, IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), 2007.

Video Presentation

[220MB]